Molecular Energies¶
Info
The importance of energies in drug design is discussed and illustrated. The different methods of calculating molecular energies are outlined and include force-field calculations in molecular mechanics.
Number of Pages: 77 (±1 hours read)
Last Modified: May 2006
Prerequisites: Molecular Geometry
Introduction¶
Internal Energy of a Molecule¶
All chemical systems contain a certain amount of internal energy consisting of potential and kinetic energies. The potential energy is directly related to chemical bonding and non-bonding interactions whereas the kinetic energy is related to random molecular motions. Each geometry (conformation) of a molecule has its specific internal energy; this is due to different non-bonding interactions.
articles
Random Walk Molecular Mechanics: RAMM - A New Procedure for Theoretical Conformational Analysis of Carbohydrates Kozar T, Petrak F, Galova Z and Tvaroska I Carb. Res. 204 1990
Internal Energy Associated to a Conformation¶
Every conformation of a molecule has an internal energy. This energy is represented by a number (in kcal/mol or in kJ/mol), which indicates if the conformation is of low, medium or high energy.
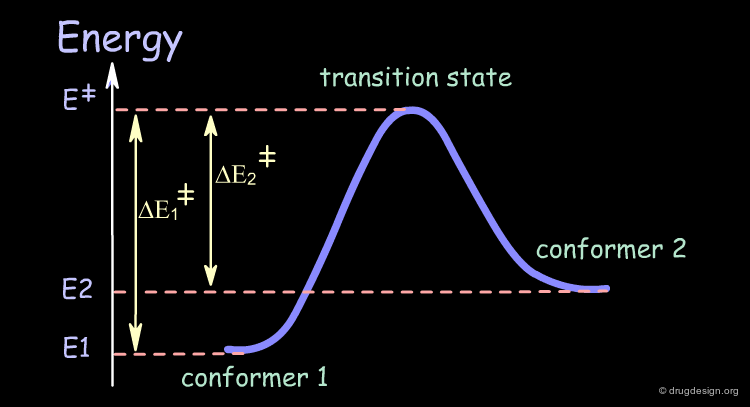
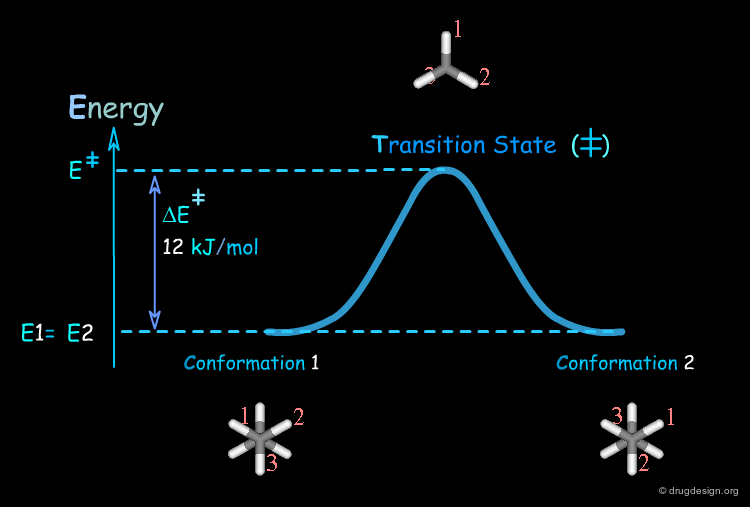
Transition State¶
The conversion of a conformer of a molecule into another one involves a high energy geometry, also known as the transition state. This high energy operates as a barrier that the molecule has to cross in order to change its three dimensional structure.
articles
Reaction Coordinates and Structure-Energy Relationships Grunwald E Prog. Phys. Org. Chem. 17 1990
Just What is a Transition State? Laidler KJ J. Chem. Education 65(6) 1988
Conformational Aspects of Inhibitor Design: Enzyme-Substrate Interactions in the Transition State Wolfenden R Bioorg. Med. Chem. 7 1999
Potential Surface¶
The following symbolic graph represents energy as a function of the structural geometrical changes of the molecule. It is also called the conformational potential surface graph.
articles
Walking in the Free Energy Hypersurface of the 18-Crown-6 Ion System Using Free Energy Derivatives Cieplak P, Pearlman DA and Kollman J. Chem. Phys. 101 1994
Reaction Coordinates and Structure-Energy Relationships Grunwald E Prog. Phys. Org. Chem. 17 1990
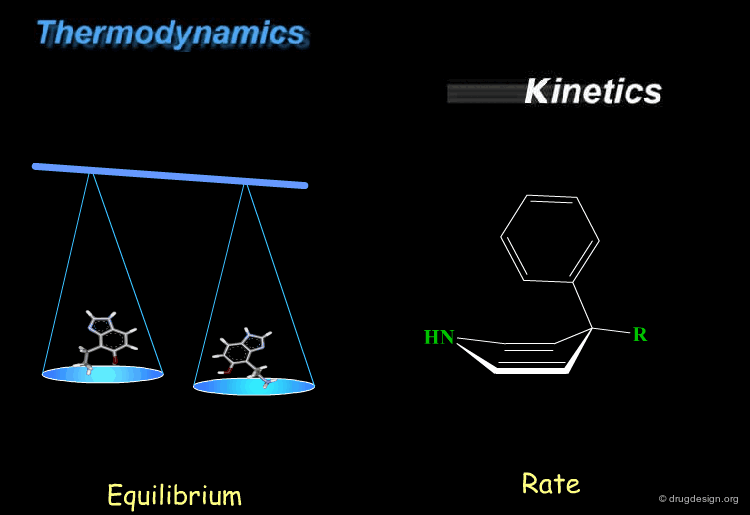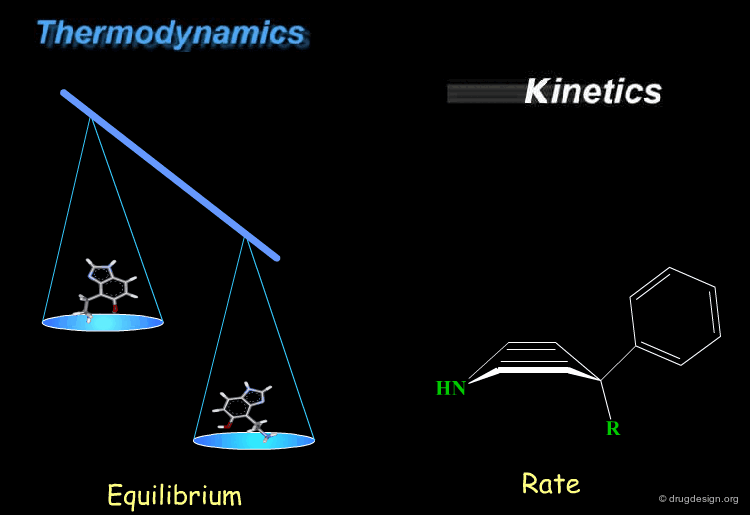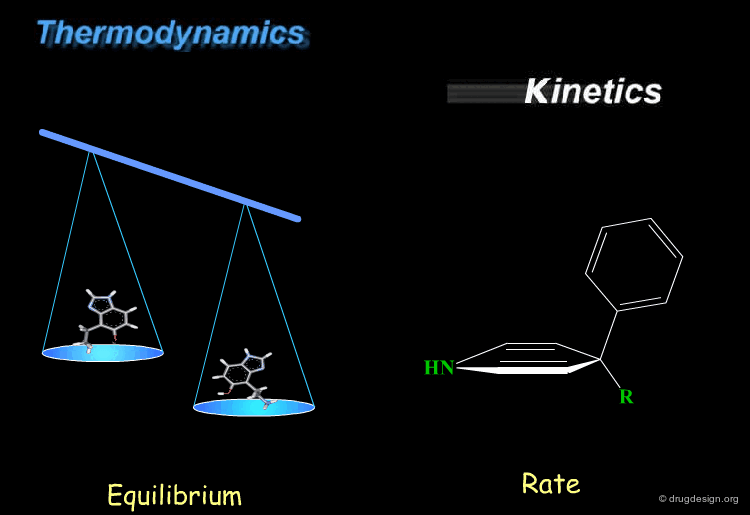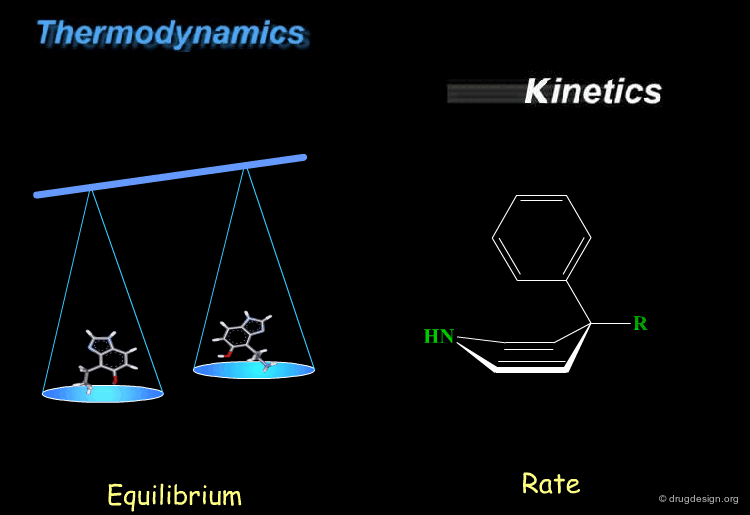
Thermodynamics & Kinetics¶
Kinetics and thermodynamics are two important concepts, which are involved in all dynamic systems. For molecules, thermodynamics define the ratio at equilibrium between molecular conformers (which conformers are possible) while kinetics define the speed (rate) of exchange from one conformation to another. These two concepts are often confused and the next pages will give some practical examples to illustrate and clarify them.
book
Laidler KJ Chemical Kinetics. 3rd Ed Harper & Row 1987
Steinfeld JI, Francisco JS and Hase WL Chemical Kinetics and Dynamics Prentice-Hall 1989
Thermodynamics¶
Thermodynamics: Conformer Populations¶
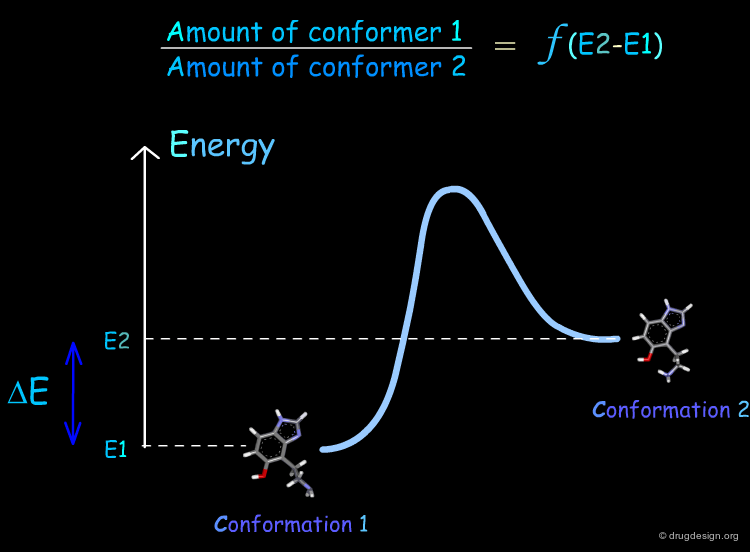
The lower the energy of a conformation of a given molecule, the more likely it is to be populated. Consider the general situation of a molecule in equilibrium in two conformational states. The population of each conformer is directly related to the difference of energy between them (E2-E1).
Thermodynamics: Boltzmann Equation¶
For a molecule existing as a mixture of conformers, the Boltzmann population equations allow us to calculate the proportion of each conformer by assuming that the conformations are in a thermodynamic equilibrium. A practical formula for calculating the percentage for each conformer present in the mixture is the following:
Boltzmann Population Analysis for Two Conformers¶
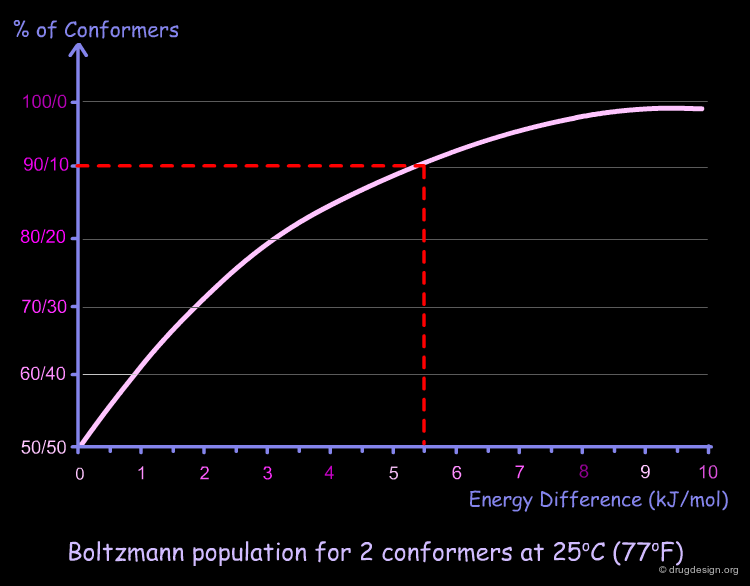
If we represent graphically the Boltzmann equation for two conformers at 25°C (77°F), we obtain the following graph. A zero energy difference corresponds to 50% population of each conformer. For example, for a difference of energy of 5.5 kJ/mol we have 90% of the low energy conformer and 10% of the high energy one.
Boltzmann Population Analysis for 3 Conformers¶
The following figure illustrates a molecule existing as a mixture of three conformers. Modify the energies of the different conformers and observe the consequences in their respective populations.
Thermodynamics: Cyclohexane Example¶
Energy¶
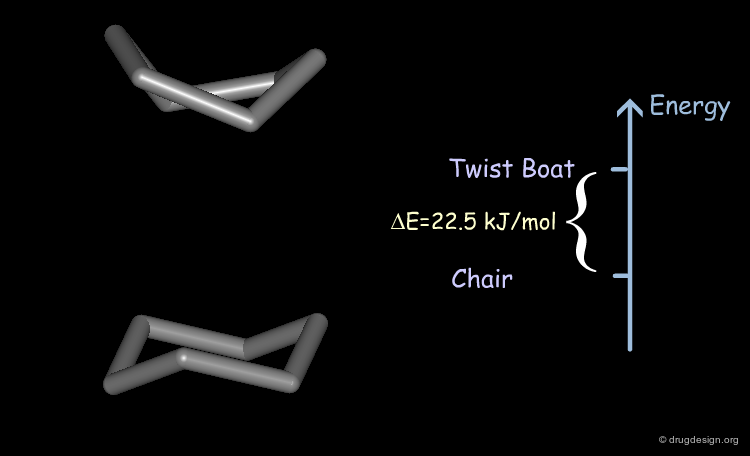
Exhaustive explorations of all the possible conformations of cyclohexane reveal two minimum energy conformations: the chair and the twist-boat. There is a difference of energy of about 22.5 kJ/mol (5.4 kcal/mol) in favor of the chair conformation.
Populations of Twisted-Boat and Chair Conformers¶
According to the Boltzmann graph, the twist-boat is 0.01% and the chair is 99.99% populated; this means that for every molecule in the twist-boat form, about 10000 molecules are in the chair conformation.
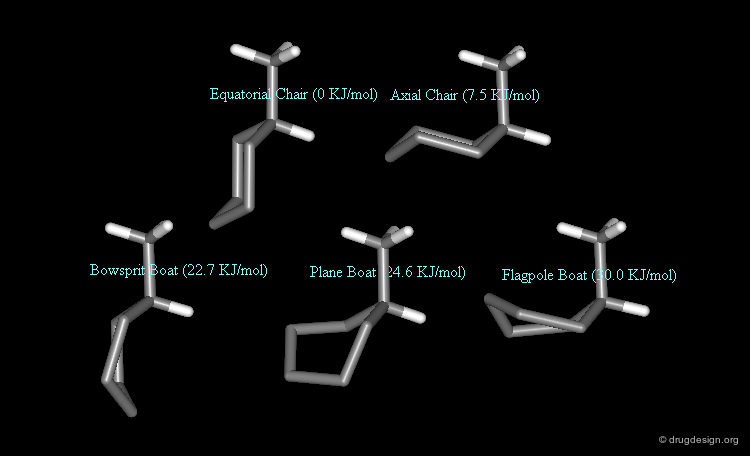
Thermodynamics: Methylcyclohexane Example¶
Methylcyclohexane has 5 different conformations. 2 chair forms (methyl in the equatorial and in the axial orientation) and 3 twist boat forms (bowsprit, flagpole and plane methyl orientation). By taking the lower energy conformer (the equatorial chair conformer) at zero energy, the energy differences and the populations of the different forms are as follows:
Kinetics¶
Kinetics¶
The answer to the question "how and how fast do conformers interconvert?" requires knowledge of the system kinetics, specifically the energy barrier between the different forms. This energy barrier is related to the geometrical (steric) and electronic changes occurring in the conformational changes and its height is a function of those changes.
Kinetics: Arrhenius Equation¶
The rate of the kinetic process can be approximated by the Arrhenius equation:
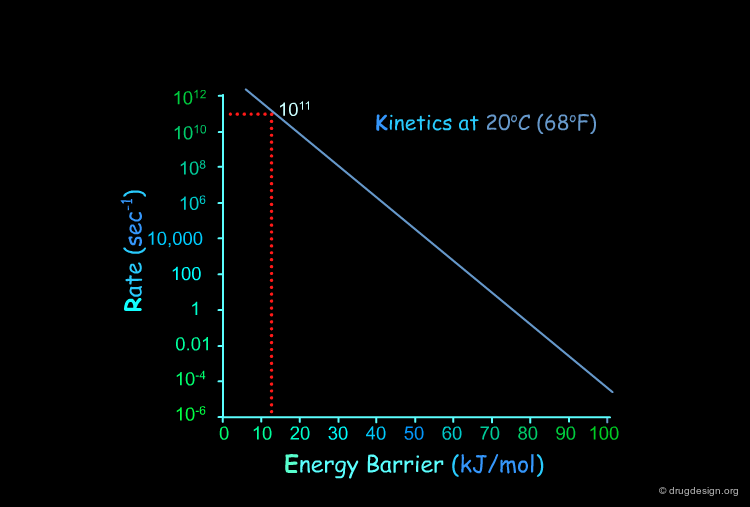
Kinetics: Arrhenius Graph¶
This figure represents the kinetic rate calculated by the Arrhenius equation at different temperatures as a function of the energy barrier. The next pages will illustrate the usefulness of these graphs.
Kinetics Ethane Example¶
At room temperature the ethane molecule has a low energy torsional barrier of about 12 kJ/mol.
Torsional Barrier in Ethane¶
The torsional barrier of 12 kJ/mol corresponds to a rate constant of about 1011 sec-1. This means that the group will cross the barrier about of 1011 times every second.
Kinetics Cyclohexane Example¶
The chair/twist-boat interconversion barrier of cyclohexane is about 45 kJ/mol.
articles
The Rate of Chair-Chair Interconversion of Cyclohexane Jensen FR, Noyce DS, Sederholm CH and Berlin AJ J. Am. Chem. Soc. 84 1962
Interconversion Barrier in Cyclohexane¶
A barrier of 45 kJ/mol corresponds to a rate constant of approximately 500,000 sec-1. This means that the barrier is crossed 500,000 times per second.
Kinetics Amide Bond Example¶
The torsional barrier of an amide bond is about 75 kJ/mol.
Amide Barrier Crossed Every 10 Seconds¶
A barrier of 75 kJ/mol corresponds to a rate constant of approximately 0.1 sec-1. This means that the barrier is crossed once every 10 seconds. This situation can be compared to the case of the double bond (rotation barrier of about 250 kJ/mol) where the barrier is crossed at room temperature once every 1024 years.
Molecular Modeling¶
Molecular Modeling¶
The good knowledge of thermodynamic and kinetic principles results in a good understanding of the thermodynamic and kinetic properties of the conformations of a molecule. Productive molecular modeling consists of not only being able to recognize such properties, but also to influence and control them in an active manner. The examples that follow illustrate how intelligent modeling can influence and control molecular behavior.
articles
Molecular Modeling Broughton HB Curr. Opin. Chem. Biol. 1 1997
Example of Kinetic or Thermodynamic Control¶
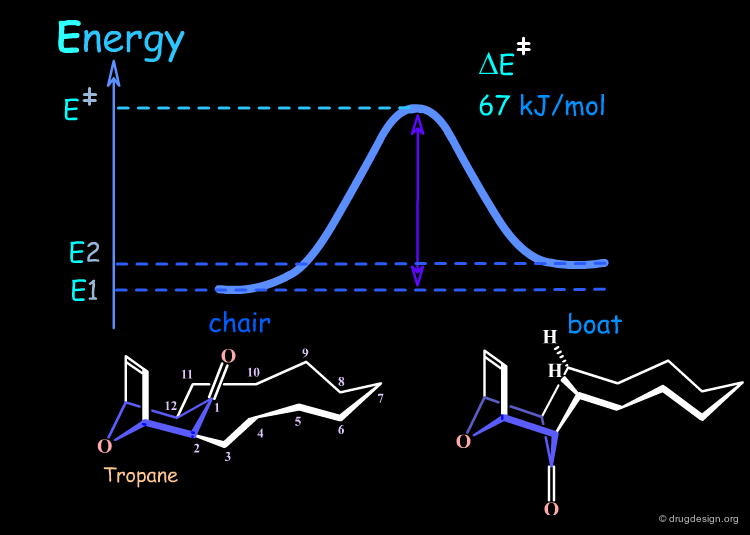
The 12-membered bridgehead ring tropane molecule displayed here has two conformers corresponding to a boat and chair tropane conformations. In non-polar solvents the chair is favored by 0.2 kJ/mol (chair 52% - boat 48%).
articles
Direct Observation of Chair-Boat Equilibria in Bridged Six-membered Rings Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 95(9) 1973
Cycloadditions of Cyclic Allyl Cations of Furan. Configuration and Conformational Analysis of the Resulting Bridged Six-membered Rings. Isolation and Identification of Boat and Chair Atropisomers Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 96(17) 1974
Interconversion Between the Two Forms¶
The energy barrier of interconversion between the two forms requires the carbonyl group to squeeze through the large ring. The energy is 67 kJ/mol, the chair-boat interconversion is possible and occurs 7 times per second. The examples that follow will illustrate how it is possible to either decrease or increase the barrier of interconversion (kinetic control) and also to modify the relative energy between the chair and the boat conformers (thermodynamic control).
Lowering the Energy of the Transition State¶
In the 13-membered ring analog (a methylene is added to the ring), there is still a small energy difference (2.7 kJ/mol) between the boat and chair conformations, the chair being preferred. However this analog has a much lower energy barrier (approximately 37 kJ/mol) as compared to the 67 kJ/mol of the 12-membered ring.
articles
Direct Observation of Chair-Boat Equilibria in Bridged Six-membered Rings Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 95(9) 1973
Cycloadditions of Cyclic Allyl Cations of Furan. Configuration and Conformational Analysis of the Resulting Bridged Six-membered Rings. Isolation and Identification of Boat and Chair Atropisomers Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 96(17) 1974
Interconversion Between the Two Forms¶
In the 13-membered ring, it is easier for the carbonyl to squeeze through the 13-membered ring and results in the decrease the interconversion energy from 67 kJ/mol to 37 kJ/mol. the chair-boat interconversion is possible at a higher rate (1,500,000 times per second instead of 7) as compared to the 12-membered ring system.
Raising the Energy of the Transition State¶
In the 11-membered ring analog the interconversion energy is 92 kJ/mol, a much higher value when compared to the 67 kJ/mol of the 12-membered ring, and the chair becomes of higher energy. The tropane moiety is frozen in the boat conformation.
articles
Direct Observation of Chair-Boat Equilibria in Bridged Six-membered Rings Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 95(9) 1973
Cycloadditions of Cyclic Allyl Cations of Furan. Configuration and Conformational Analysis of the Resulting Bridged Six-membered Rings. Isolation and Identification of Boat and Chair Atropisomers Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 96(17) 1974
Interconversion Between the Two Forms¶
Due to the high energy barrier, the tropane moiety is found only in a boat conformation. At room temperature the chair conformer cannot be seen by NMR, the chair-boat interconversion is virtually not possible.
Modifying Conformers Populations¶
Let us analyze what happens to the boat atropisomer of the 11-membered ring (that can be isolated) if we reduce the double bond to a single bond. Molecular models reveal to us that strong steric interactions are created in the reduced molecule.
articles
Direct Observation of Chair-Boat Equilibria in Bridged Six-membered Rings Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 95(9) 1973
Cycloadditions of Cyclic Allyl Cations of Furan. Configuration and Conformational Analysis of the Resulting Bridged Six-membered Rings. Isolation and Identification of Boat and Chair Atropisomers Vinter JG and Hoffmann HMR J. Am. Chem. Soc. 96(17) 1974
Repulsions More Important in the Boat Form¶
Analysis of the steric interactions in the boat and the chair conformers indicate that the repulsions are more important in the boat form. The chair conformer is likely to be of lower energy and be the preferred conformation.
Tropane is Found Only in a Chair Conformation¶
NMR analyses show that in the reduced 11-membered ring the tropane moiety is found only in a chair conformation. At room temperature the boat conformer cannot be seen, while the interconversion barrier remained unchanged. The chair-boat interconversion is virtually not possible.
Example of Atropisomerism¶
We have here an example of two compounds (the olefin and the reduced molecule) which differ in the conformation of the six-membered ring. One compound being only in a boat and the other only in a chair atropisomer.
Molecular Energies: The Key of Molecular Modeling¶
We showed in the previous examples how it is possible to control activation energies and conformational population. From the point of view of modeling, the basic task remains the same and consists of influencing (decreasing or increasing) the energy of a given form (such as a transition state or a conformation) without altering other forms.
Modeling in Drug Design¶
Molecular Modeling in Drug Design¶
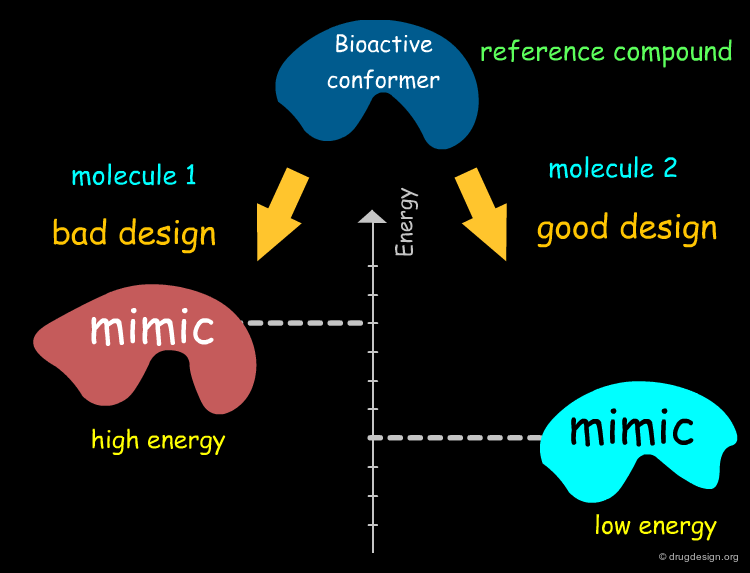
Let's assume we know the bioactive conformation of a specific biomolecule.
One of the main goals in the design of a new drug is to conceive a structure for which the conformation that mimics the bioactive form of the reference compound is of low energy and therefore this increases the chance of having an active compound.
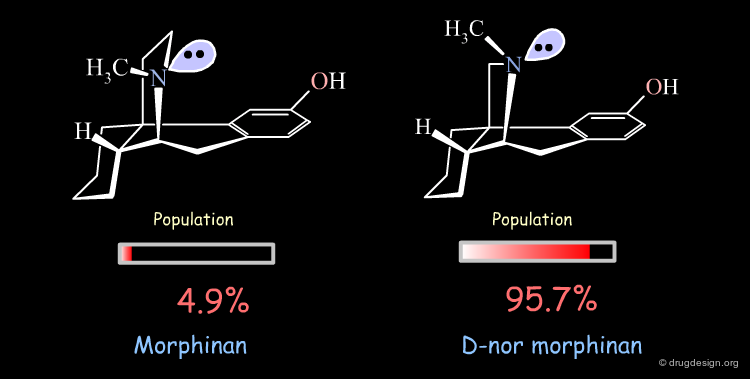
Importance of Energies: the Morphinan Example¶
Morphinan is a substance of the morphine alkaloids family with analgesic properties. However, removing one carbon from the piperidine ring (converting it to a pyrrolidine ring) gives an entirely inactive molecule, D-nor morphinan.
articles
Drug Design in Three Dimensions Cohen NC Advances in Drug Research 14 1985
Importance of the Nitrogen Lone Electron Pair Orientation in Stereospecific Opiates Belleau B, Conway T, Ahmed FR and Hardy AD J. Med. Chem. 17 1974
book
Dimaio J, Ahmed FR, Schiller P and Belleau B Recent Advances in Receptor Chemistry Elsevier 1979
Morphinan and D-nor Morphinan Alignment¶
When 3D models of the two molecules are constructed, they prove to be almost superimposable. Are the small differences we see in the view sufficient for accounting the large differences we observe in the biological activities? To answer that question, additional analyses are necessary to better assess and understand the exact stereochemical requirements for binding to the receptor.
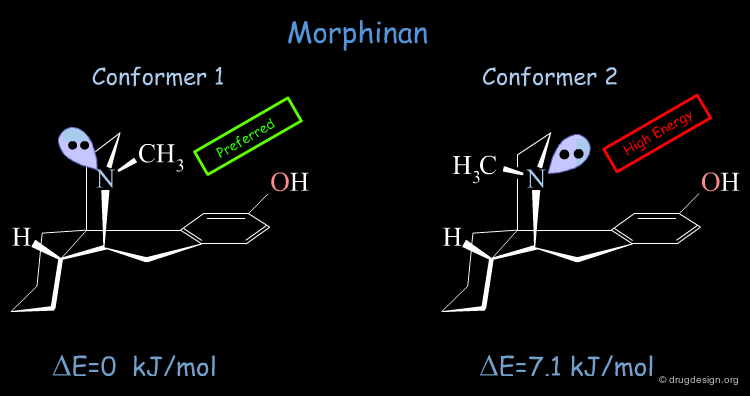
Conformational Analysis of Morphinan¶
The conformational analysis of Morphinan (based on force-field calculations and minimization techniques) shows that the molecule exists in two conformational states. The low energy form was found to have the nitrogen lone pair oriented away from the aromatic ring. The second form which is energetically higher by 7.1 kJ/mol has the nitrogen lone-pair pointing towards the aromatic phenolic ring.
articles
Importance of the Nitrogen Lone Electron Pair Orientation in Stereospecific Opiates Belleau B, Conway T, Ahmed FR and Hardy AD J. Med. Chem. 17 1974
Drug Design in Three Dimensions Cohen NC Advances in Drug Research 14 1985
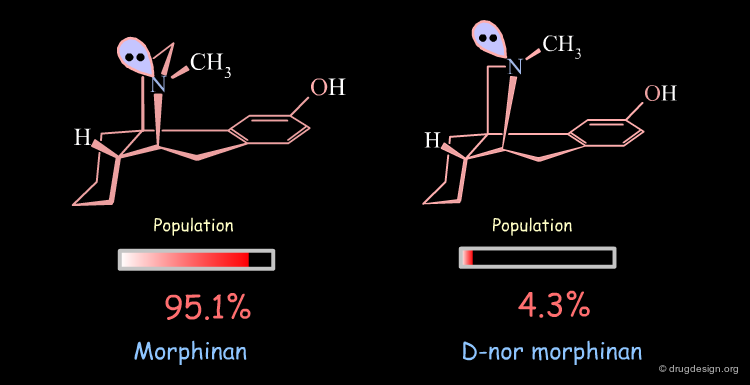
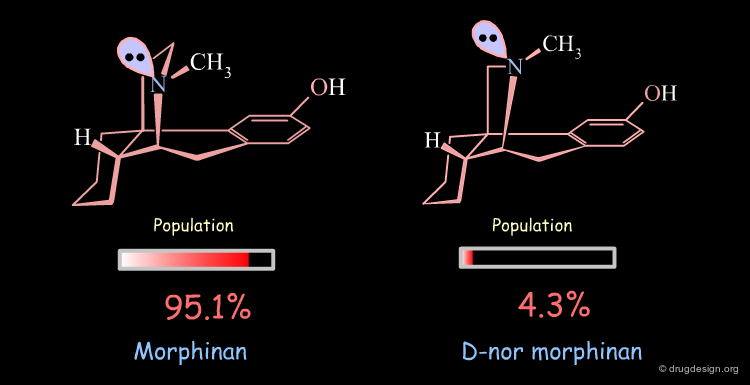
Conformational Analysis of D-nor Morphinan¶
A similar analysis made on d-nor morphinan shows that this compound also exists in two conformational states. However, the low energy conformation was found to have the nitrogen lone pair oriented towards the aromatic ring, and the second form which is 7.53 kJ/mol higher in energy has the nitrogen lone pair oriented away from the aromatic ring; a reverse situation when compared to morphinan.
articles
Drug Design in Three Dimensions Cohen NC Advances in Drug Research 14 1985
A Rationale for Explaining the Activities Observed¶
The orientation of the nitrogen lone pair is the key to interpret the biological activities observed. A good recognition by the receptor may require this lone pair to be oriented away from the benzene ring. D-nor morphinan would be active if the conformer with the lone-pair oriented away from the aromatic ring would be populated enough, but with such an energy difference (7.53 kJ/mol) it is not sufficiently populated (4.3%).
articles
Drug Design in Three Dimensions Cohen NC Advances in Drug Research 14 1985
Morphinan: Validation and Design¶
In order to validate the hypothesis that the lone pair of the nitrogen atom must be oriented away from the phenolic fragment, the 16,17 butanomorphinan was prepared and the two enantiomeric molecules were separated. In one of them the lone pair was in the "proper" orientation, whereas in the second one the lone pair was oriented in the opposite direction. The molecule with the lone pair oriented away from the benzene ring proved to be active; the second enantiomer was inactive. Information on the conformations of the two enantiomers is given in the next pages.
articles
Structural differences between 16α, 17-butanomorphinan-3-ol and 16β,17-butanomorphinan-3-ol Ahmed FR Acta Cryst. B37 1981
Drug Design in Three Dimensions Cohen NC Advances in Drug Research 14 1985
X-ray analytical reexamination of correlation of nitrogen lone-pair orientation with analgetic activity Shiotani S, Kometani T, Iitaka Y and Itai A J. Med. Chem. 21 1978
book
Dimaio J, Ahmed FR, Schiller P and Belleau B Recent Advances in Receptor Chemistry Elsevier 1979
Preferred Conformer of Active Enantiomer¶
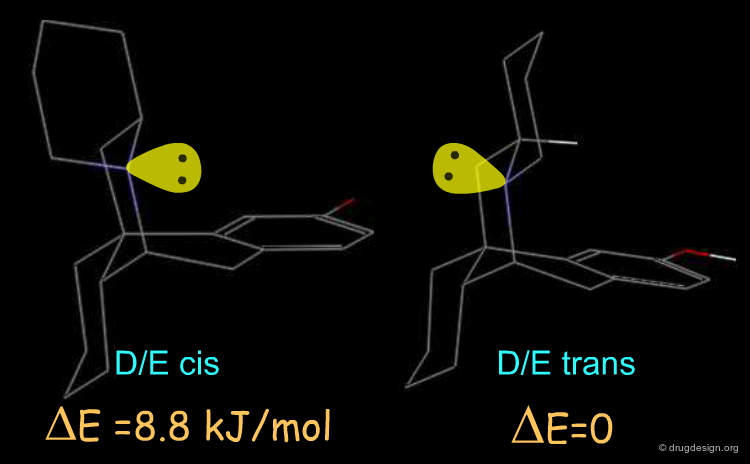
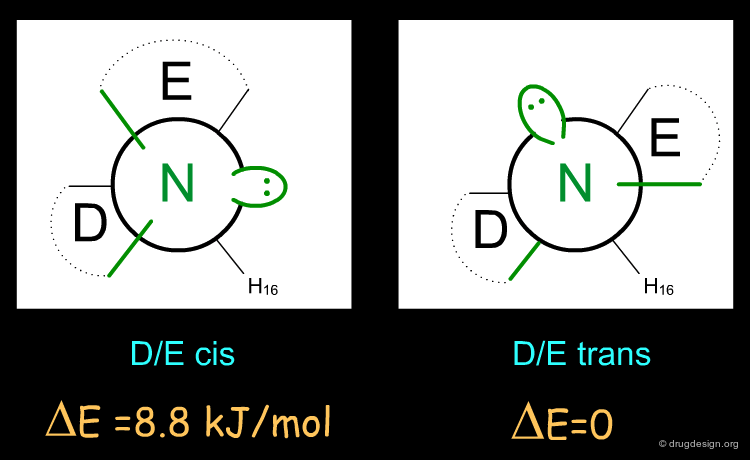
The active enantiomer of 16,17 butanomorphinan has a stereochemistry with H16 down. This compound can exist in two alternative all-chair conformations with the D/E fusion being either cis or trans (lone pair either gauche or anti, relative to the angular hydrogen H16). Force field minimizations indicate that the trans system is more stable than the cis, and this corresponds to a geometry where the lone pair is oriented away from the aromatic A-ring.
Preferred Conformer of Inactive Enantiomer¶
Two alternative conformations can be considered for this enantiomer. The first is in an all chair conformation and a cis D/E fusion (lone pair and H16 gauche); however it has a high energy because of steric clashes with the axial hydrogen atoms of ring E. The second one has a trans D/E fusion (lone pair and H16 anti) with however a boat geometry for ring D. Despite the unfavorable energy of the boat, this conformer is preferred due to the relief of the steric interactions with the axial hydrogen atoms. Force field minimizations show that there is a difference of 9.6 kJ/mol in favor of the boat conformer, which corresponds to a lone pair oriented towards the aromatic A-ring.
Restoring Activities to the Inactive Analog?¶
One could think of ways to restore biological activities to the D-nor morphinan series, for example by introducing appropriate substituents. Before synthesizing new molecules one could identify analogs that are worth being synthesized based on computerized molecular mechanics and force field minimizations.
Morphinan Browser¶
What We Can Learn From The Morphinan Example¶
From the morphinan example we learned the following: An elementary observation has to be fully exploited. Simple analyses are not sufficient; they must be challenged. One should never underestimate the importance of energies. The analyses can provide insights in the binding to the receptor and in the mechanism of action. A good analysis generates creative conditions for conceiving new compounds. New molecules allow us to validate and refine the model considered. Finally, an elementary observation can be of high informational content.
How to Calculate Energies¶
The Need of Tools for Calculating Energies¶
We saw that molecular energies are of key importance in molecular modeling and drug design. Appropriate computerized tools are necessary to access such information.
Two Methods for Calculating Energies¶
There are two main computational methods for calculating the energy of a molecule or a set of molecules: quantum mechanics and molecular mechanics methods.
Quantum Mechanics¶
Calculation of Energies by the Schrodinger Equation¶
In quantum mechanics, the energy of a given system (a molecule or sets of molecules) is obtained by solving the Schrodinger equation that defines the wave function of the molecular system. In principle, this wave function contains all the information needed to describe the properties of the system, including its total energy.
Ab-Initio and Semi-empirical Calculations¶
The Schrodinger equation can be solved either with no approximations at all (ab-initio) or with the introduction of some approximations (semiempirical). An exact solution is today an impossible mathematical problem for small molecular systems; however, acceptable approximate solutions may be obtained with semiempirical methods for calculating the conformations of molecules with several hundreds of electrons. One way to approximate is to treat only the valence electrons (and not all of them as in ab initio methods) for the construction of atomic orbitals.
articles
Ground States of Molecules. XXV. MINDO/3. An Improved Version of the MINDO Semiempirical SCF-MO Method Bingham RC, Dewar MJS and Lo DH J. Am. Chem. Soc. 97(6) 1975
AM1: A New General Purpose Quantum Mechanical Molecular Model Dewar MJS, Zoebisch EG, Healy EF and Stewatr JJP J. Am. Chem. Soc. 107(13) 1985
Basis Sets for AB initio Molecular Orbital Calculations and Intermolecular Interactions Feller D and Davidson ER Reviews in Computational Chemistry 1 1990
Semiempirical Methods: Current Status and Aerspectives Thiel W Tetrahedron 44(24) 1988
book
Dykstra CE AB Initio Calculation of the Structure and Properties of Molecules Elsevier Science Publishers Inc 1988
Hehre WJ, Radom L, Schleyer PvR and Pople JA AB Initio Molecular Orbital Theory John Wiley & Sons Inc 1986
Richards WG and Cooper DL AB Initio Molecular Orbital Calculations for Chemists. 2nd Ed Oxford University Press 1983
Szabo A and Ostlund NS Modern Quantum Chemistry Introduction to Advanced Electronic Structure Theory McGraw-Hill Publishing Co 1989
Calculation of Energies¶
Energies of a specific geometry are calculated with "self consistent field" methods (SCF) where the approximate initial wave function is iteratively modified until the total energy does not decrease. Full geometry optimization therefore requires two types of minimization: one for the calculation of the energies (SCF calculations) and one for the optimization of the geometries.
The Density Function Theory¶
The recently developed density functional methods are a valuable alternative to ab initio quantum chemical calculations. Still based on the SCF theory, the density function theory uses the electron density as the variable of the system instead of the electronic wavefunction as in the traditional Hartree-Fock formalism. This can be done without loss of rigor and leads to a substantial reduction of the computational effort.
articles
An Introduction to Density Functional Theory Bartolotti LJ and Flurchick K Reviews in Computational Chemistry 7 1995
The Choice of a Method¶
In practice only molecules containing less than about 70 - 80 atoms can be calculated with quantum mechanical approaches. The choice of the method is strongly dictated by the size of the system to be studied, the availability of adequate computer software and hardware and the expertise for the analysis and interpretation of the results. They unfortunately drastically reduce the possibility that such approaches can offer.
articles
Molecular Modeling Methods. Basic Techniques and Challenging Problems Lesyng B and McCammon JA Pharmac. Ther. 60 1993
Molecular Mechanics¶
Molecular Mechanics¶
Molecular mechanics is an approach based on the idea that the atoms of the molecule feel forces and the energy of a conformation is related to these forces.
book
Burkert U and Allinger NL olecular Mechanics
Washington, DC
Burt SK, Mackey D and Hagler AT Computer-Aided Drug Design. Methods and Applications Marcel Dekker 1989
Force-Field¶
An empirical set of energy functions called force field allows simulation of such forces. Molecular mechanics calculations are fast and rather accurate.
articles
Conformational Analysis. 130. MM2. A Hydrocarbon Force Field Utilizing V1 and V2 Torsional Terms Allinger NL J. Am. Chem. Soc. 99(25) 1977
Molecular Mechanics: The MM3 Force Field for Hydrocarbons. 1 Allinger NL, Yuh YH and Lii JH J. Am. Chem. Soc. 111(23) 1989
The MM3 Force Field for Alkenes Allinger NL, Li F and Yan L J. Comput. Chem. 11 1990
Empirical Force Field Calculations: A Tool in Structural Organic Chemistry Altona C and Feber DH Top. Curr. Chem. 45 1974
Consistent Force Field Calculation of Conformation, Vibrational Spectra, and Enthalpies of Cycloalkane and n-Alkane Molecules Lifson S and Warshel A J. Chem. Phys. 49(11) 1968
MacroModel- An Integrated Software System for Modeling Organic and Bioorganic Molecules Using Molecular Mechanics Mohamadi F, Richards NGJ, Guida WC, Liskamp R, Lipton M, Caufield C, Chang G, Hendrickson T, and Still WC J. Comp. Chem. 11 1990
Conformational Energy Calculations on Polypeptides and Proteins Vasquez M, Nemethy G and Scheraga HA Chem. Rev. 94 1994
Consistent Force Field Calculation. II. Crystal structure, sublimation energies, molecular and lattice vibrations, molecular Conformations, and Enthalpies of Alkanes Warshel A and Lifson S J. Chem. Phys. 53(2) 1970
AMBER: Assisted Model Building with Energy Refinement. A General Program for Modeling Molecules and their Interactions Weiner PK and Kollman PA J. Comp. Chem. 2 1981
A New Force Field for Molecular Mechanical Simulation of Nucleic Acids and Proteins Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, Alagona G, Profeta S and Weiner P J. Am. Chem. Soc. 106 1984
An All Atom Force Field for Simulations of Proteins and Nucleic Ccids Weiner SJ, Kollman PA, Nguyen DJ and Case DA Journal of Computational Chemistry 7(2) 1986
Force Field Components¶
A typical force field consists of bond stretching, angle bending, torsional rotation, van der Waals interaction, electrostatic interaction, and hydrogen bonding energy functions. The energy of a conformer is the total sum of all those contributions.
articles
Conformational Analysis. 130. MM2. A Hydrocarbon Force Field Utilizing V1 and V2 Torsional Terms Allinger NL J. Am. Chem. Soc. 99(25) 1977
Molecular Mechanics: The MM3 Force Field for Hydrocarbons. 1 Allinger NL, Yuh YH and Lii JH J. Am. Chem. Soc. 111(23) 1989
The MM3 Force Field for Alkenes Allinger NL, Li F and Yan L J. Comput. Chem. 11 1990
Computer Modeling of Protein Structures: Energy Minimization as a Tool for the Design of Novel Molecules Barba D, He Z and Marrelli L Rev. Chem. Eng. 7 1991
Appendix: Published Force Field Parameters for Molecular Mechanics, Molecular Dynamics, and Monte Carlo Simulations Jalaie M and Lipkowitz KB Reviews in Computational Chemistry 14 2000
Bond Lengths: Stretching Contributions¶
A chemical bond between two atoms has a "natural" equilibrium position. The bond is considered as a spring and an energy penalty is associated with any change of the bond length.
Function¶
The stretching energies are expressed by the following equation (Hook's law). The stretching force constants are determined experimentally from vibration spectroscopy.
Examples of Elementary Stretching Contributions¶
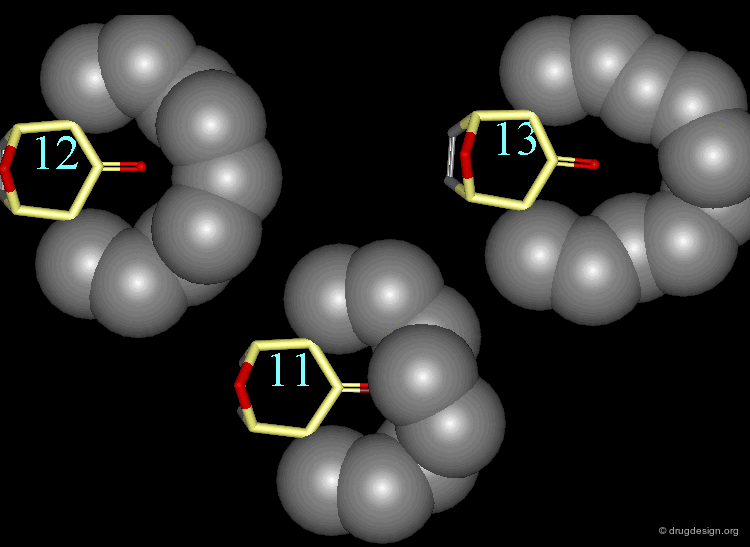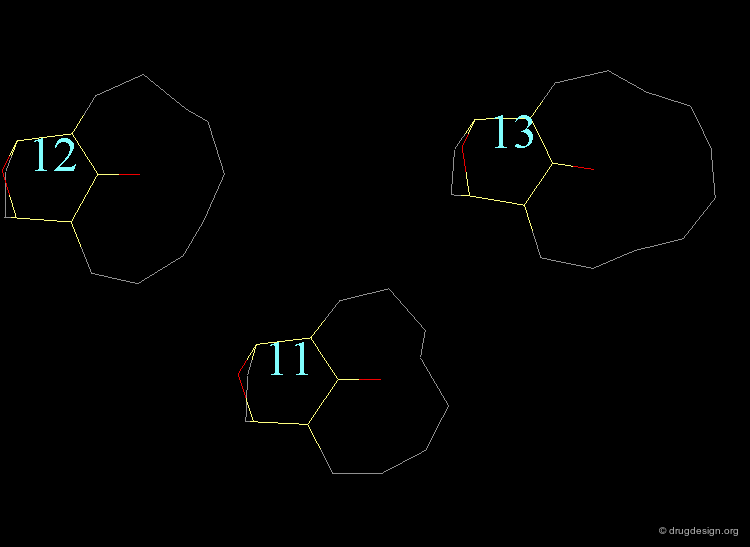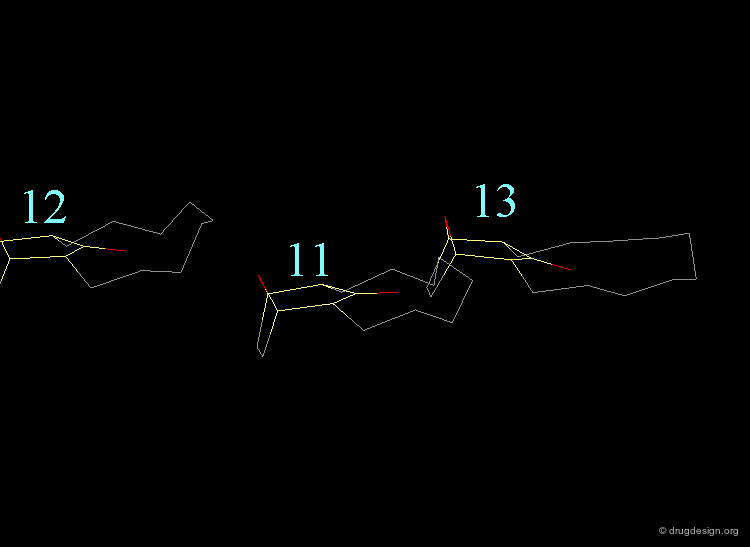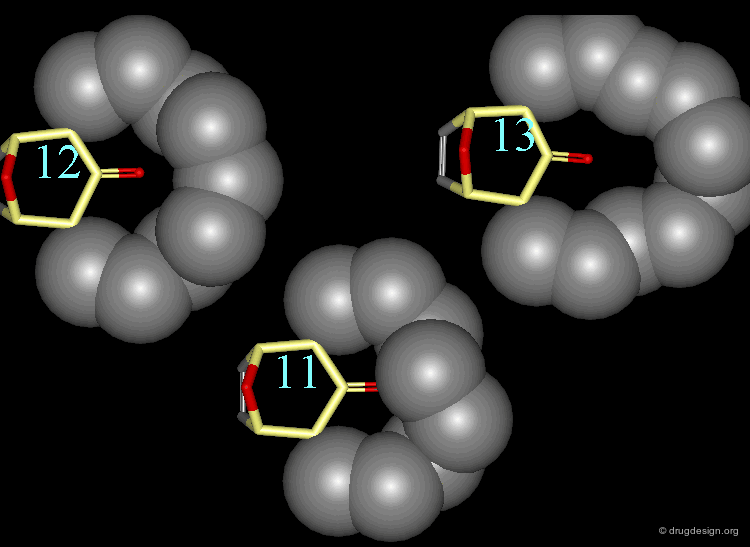
The stretching contributions existing in the following molecule are detailed. For each pair of atoms the theoretical and the actual bond lengths are shown, as well as the elementary strain energy associated to the stretching of the bond.
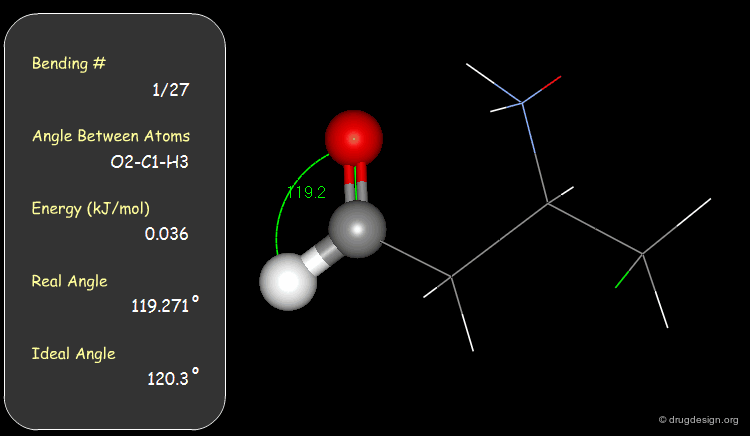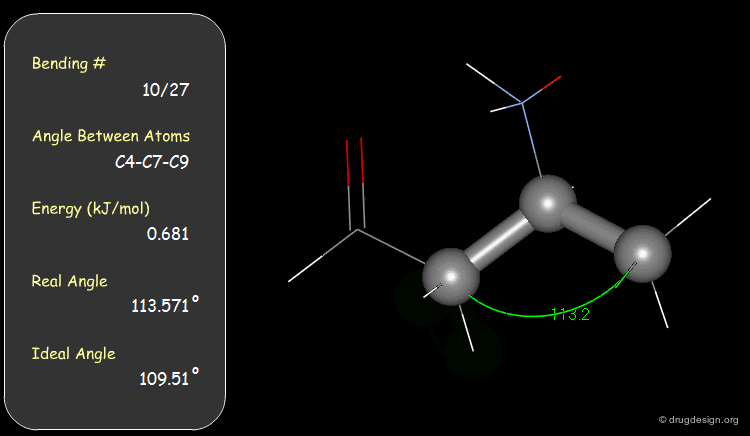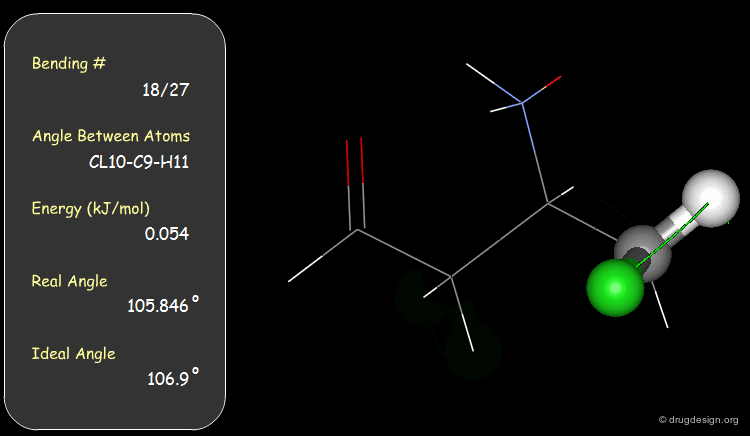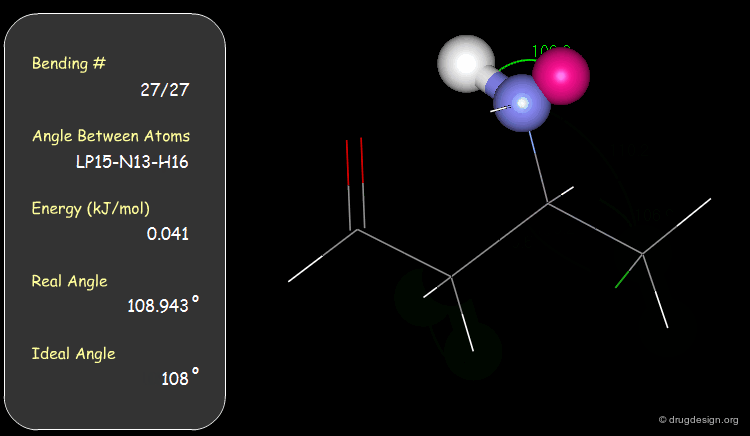
Bond Angles: Bending Contributions¶
The valency angle between three atoms has a "natural" equilibrium position. An energy penalty is associated with any change of the bond angle from its equilibrium value.
Function¶
The bending energies are expressed by the following equation. The bending force constants are determined experimentally from vibration spectroscopy.
Examples of Elementary Bending Contributions¶
The bending contributions existing in the following molecule are detailed. For each valency angle the theoretical and the actual bond angles are shown, as well as the elementary energy associated to the strain.
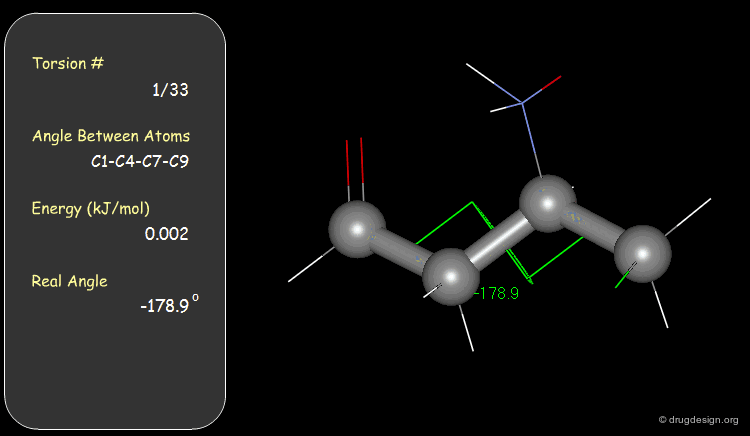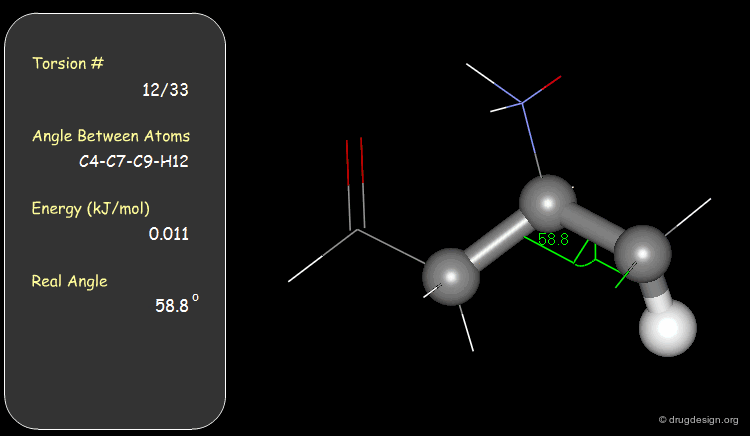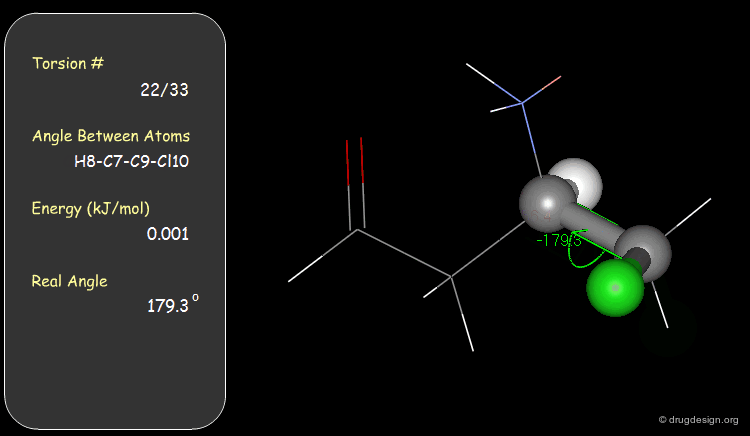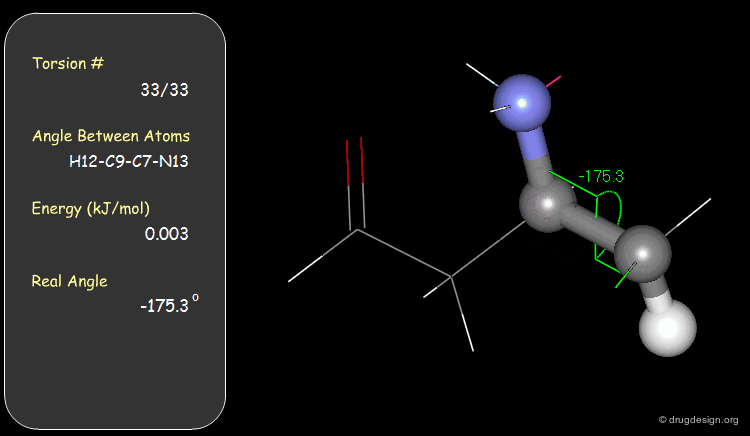
Torsion Angles: Torsional Contributions¶
An energy is associated with each torsion angle. The origin of this energy is through-space steric and electronic interactions between non-bonded atoms.
Function¶
The torsional energies are expressed by a Fourier series as a function of the torsion angle (Φ). The barriers (Vi) can be obtained experimentally (e.g. microwave spectroscopy) or by theoretical calculations (e.g. Gaussian).
Examples of Elementary Torsional Contributions¶
The torsional contributions existing in the following molecule are detailed. For each torsion angle the value of the angle is shown together with the elementary energy associated to this situation.
Van der Waals Interactions¶
Interactions exist between non-bonded atoms and are called 'van der Waals' interactions. At a short distance, there is repulsion between the two atoms (due to the interpenetration of their electronic clouds), and at a long distance, there is a small attraction (dispersion forces).
articles
Van der Waals Volumes and Radii Bondi A J. Phys. Chem. 68(3) 1964
Theoretical Studies of van der Waals Molecules and Intermolecular Forces Buckingham AD, Fowler PW and Hutson JM Chem. Rev. 88 1988
Function¶
There are a variety of mathematical equations used for calculating van der Waals interactions (Morse, Buckingham, Lennard-Jones). The following equation corresponds to the Lennard-Jones Potential.
Examples of Elementary Van der Waals¶
The van der Waals contributions existing in the following molecule are detailed. For each pair of non-bonded atoms the actual distance is shown, as well as the elementary energy associated to the interaction.
Electrostatic Dipolar Contributions¶
Interaction between polar atoms or bonds may result in attractions or repulsions.
Function¶
The interaction energy between two polar bonds can be calculated with the following formula:
Examples of Elementary Electrostatic Contributions¶
The electrostatic contributions existing in the following molecule are detailed. For each pair of polar atoms the actual distance is shown, as well as the elementary energy associated to the interaction.
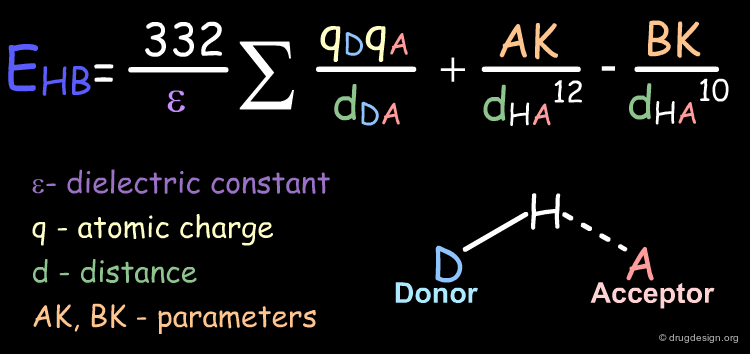
Hydrogen Bond Energy Contributions¶
A hydrogen bond is an attractive interaction between a hydrogen atom that is covalently bonded to an electronegative element and a second electronegative element. Note that the energy of a strong hydrogen bond is between 12-21 kJ/mol while the energy of a covalent bond is about 418 kJ/mol.
articles
Binding Energy of an Amide-Amide Hydrogen Bond in Aqueous and Nonpolar Solvents Doig AJ and Williams DH J. Am. Chem. Soc. 114 1992
Intermolecular Electrical Interaction: A Key Ingredient in Hydrogen Bonding Dykstra CE Acc. Chem. Res 21 1988
50 Years of Hydrogen Bond theory Huggins ML Angew. Chem. Int. Ed. Ingl. 10(3) 1971
Hydrogen Bonding and Proton Transfer Joesten MD J. Chem. Education. 59(5) 1982
The Theory of the Hydrogen Bond Kollman PA and Allen LC Chem. Rev. 72(3) 1972
Hydrogen-Bond Geometry in Organic Crystals Taylor R and Kennard O Acc. Chem. Res. 17 1984
Function¶
Hydrogen bond contributions can be calculated with the following formula:
Examples of Elementary Hydrogen Bond Contributions¶
This is an example of hydrogen bond contribution in a molecule. In the following example, only one intra-molecular hydrogen bond is possible. The distance between the hydrogen bond acceptor atom (oxygen) and the hydrogen atom of the donor group (amino) is indicated as well as the energy associated to the specific relative orientation of the two groups.
Total Energy in a Force Field Calculation¶
Force field calculations are based on 3D coordinates and calculate the energy of the corresponding conformation. Here is shown a typical result of a force field calculation.
Main Force Fields¶
Numerous force fields exist today as a result of the simultaneous development made by many groups. When dealing with molecules such as small molecules, proteins, polymers, metal containing complexes and others, it is important to choose a force field that was developed and calibrated on the type of structures concerned.
articles
Conformational Analysis. 130. MM2. A Hydrocarbon Force Field Utilizing V1 and V2 Torsional Terms Allinger NL J. Am. Chem. Soc. 99(25) 1977
Molecular Mechanics: The MM3 Force Field for Hydrocarbons. 1 Allinger NL, Yuh YH and Lii JH J. Am. Chem. Soc. 111(23) 1989
The MM3 Force Field for Alkenes Allinger NL, Li F and Yan L J. Comput. Chem. 11 1990
Supercomputing and Drug Discovery Research Boyd DB and Milosevich SAF Perspectives in Drug Discovery and Design 1 1993
Computer Modeling of Protein Structures: Energy Minimization as a Tool for the Design of Novel Molecules Barba D, He Z and Marrelli L Rev. Chem. Eng. 7 1991
CHARMM: A Program for Macromolecular Energy, Minimization, and Dynamics Calculations Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, and Karplus M J. Comp. Chem. 4 1983
Molecular Mechanics: The MM3 Force Field for Hydrocarbons. 2. Vibrational Frequencies and Thermodynamics Lii JH. And Allinger NL J. Am. Chem. Soc. 111(23) 1989
Molecular Mechanics: The MM3 Force Field for Hydrocarbons. 3. The Van der Waals' Potentials and Crystal Data for Aliphatic and Aromatic Hydrocarbons Lii JH. And Allinger NL J. Am. Chem. Soc. 111(23) 1989
MacroModel- An Integrated Software System for Modeling Organic and Bioorganic Molecules Using Molecular Mechanics Mohamadi F, Richards NGJ, Guida WC, Liskamp R, Lipton M, Caufield C, Chang G, Hendrickson T, and Still WC J. Comp. Chem. 11 1990
The MMP2 Calculational Method Sprague JT, Tai JC, Yuh Y and Allinger NL J. Comput. Chem. 8 1987
AMBER: Assisted Model Building with Energy Refinement. A General Program for Modeling Molecules and their Interactions Weiner PK and Kollman PA J. Comp. Chem. 2 1981
A New Force Field for Molecular Mechanical Simulation of Nucleic Acids and Proteins Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, Alagona G, Profeta S and Weiner P J. Am. Chem. Soc. 106 1984
An All Atom Force Field for Simulations of Proteins and Nucleic Ccids Weiner SJ, Kollman PA, Nguyen DJ and Case DA Journal of Computational Chemistry 7(2) 1986
What One Should Remember¶
Each conformation of a molecule or a system corresponds to a given energy. A force field can be considered as a black box, receiving the molecular system as input and providing in output the corresponding energy.
articles
Abuses of Molecular Mechanics. Pitfalls to Avoid Lipkowitz BK J. Chem. Educ. 72 1995
Relative Energies¶
The energies obtained by different methods have absolute values that are meaningless. They are useful only when comparing the values obtained for different geometries of the same system. Not only should one not compare the numbers obtained for the energies from one program to another, but for a given program, the energy calculated for a molecule must not be compared to the energy calculated for another molecule (except in closely related systems, such as isomers).
Copyright © 2024 drugdesign.org